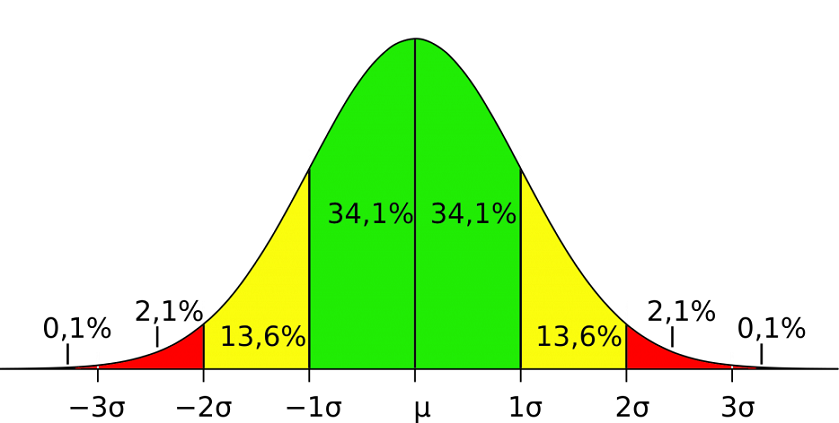
Kiểm tra bề mặt
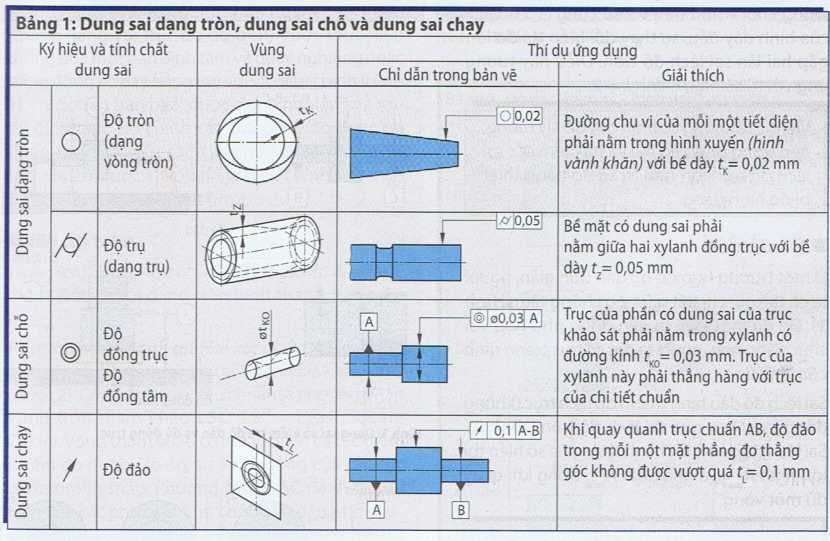
Bề mặt thật cho thấy có sai lệch với chất lượng bề mặt đã được quy định trong bản vẽ vì điều kiện sản xuất (Bảng 1).
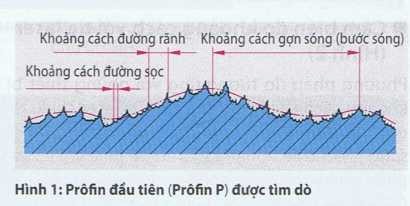
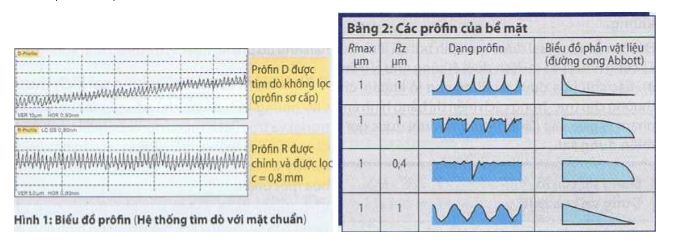
Prôfin được rà (prôfin sơ cấp/đầu tiên) cho thấy bể mặt với tất cả sai lệch đã được tìm dò với đầu tiếp xúc bằng kim cương (Hình 1). Đường trung bình của prôfin được máy tính tạo thành sao cho phần prôfin ở trên đường trung bình bằng với phần prôfin ở dưới.
Prôfin sơ cấp được tìm dò là cơ sở đầu tiên cho prôfin gợn sóng và độ nhám của prôfin cũng như cho các thông số của độ nhám. Phép đo được thực hiện trong phạm vi bề mặt (phẳng), trên phạm vi đó dự kiến là sẽ có độ nhám hoặc độ gợn sóng cao nhất. Không sử dụng phép đo ở bề mặt bị hư hỏng vì xước hoặc móp.
Nguyên lý đo Profin bề mặt
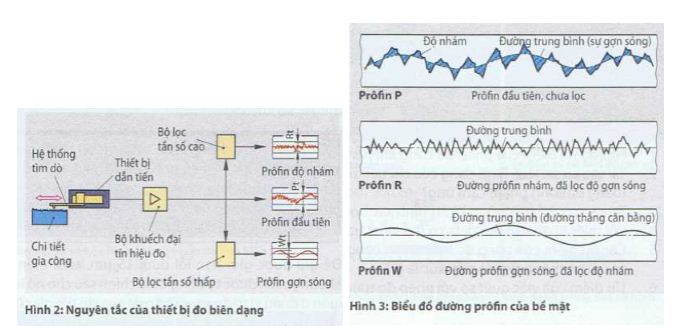
Thiết bị đo biên dạng chuyển đổi sự di chuyển của đầu dò bằng kim cương thành tín hiệu điện. Nó thu nhận prôfin và tính ra các thông số độ sâu của prôfin Pt, độ sâu của sự gợn sóng Wt, và chiều cao nhấp nhô Rt (Hình 2).Trong biểu đồ của prôfin sự sai lệch ở chiều thẳng đứng được hiện thị phóng lớn lên (Hình 3). Vì vậy các cạnh sườn của biểu đồ trông có vẻ dốc hơn so với sự thật.
Sự phóng đại ở chiều thẳng đứng của các biểu đồ được chọn sao cho prôfin bằng khoảng 1/2 chiều cao của biên bản đo.
Qua bộ lọc prôfin , người ta sẽ tìm được từ prôfin đầu tiên chưa lọc (Prôfin P) profin nhám (Prôfin R) và prôfin gợn sóng (Prôfin W) (Hình 3).
Từ prôfin sơ cấp được tìm dò, bộ lọc prôfin tách thành phần sóng ngấn của độ nhám với thành phần sóng dài của độ gợn sóng. Các thông số vể bề mặt đa số được tìm ra từ prôfin độ nhám (Profin R).
Prôfin độ nhám (Profin R) được thành lập từ prôfin sơ cấp đượctìm dò khi qua bộ lọc tần số cao, trong đó thành phần gợn sóng bị loại bỏ (Hình 2 và Hình 3). Prôfin gợn sóng (Prôfin W) được thành lập khi qua bộ lọc tần sổ thấp, trong đó thành phần độ nhám bị lọc ra.
Những thông số đặc trưng của bề mặt
Các thông số có thể được tính toán từ prôfin của bề mặt, các thông số này được đánh dấu bằng các chữ hoa P, Wvà R, thí dụ như Pt là độ sâu của prôfin P, Wt là độ sâu của prôfin gợn sóng W và Rz là prôfin độ nhám. Có rất nhiều thông số về độ nhám (Độ nhẵn bóng bề mặt), ở đây chỉ đi ngắn vào các thông số quan trọng.
■ Các thông số độ nhám theo quy ước
Những thông số độ nhám theo ISO đã được phổ biến rộng rãi như Ra, Rz và Rt và Rmax tuy đã được ISO thay thế bằng Rt nhưng vẫn còn được sử dụng.
Chiều cao nhấp nhô (chiều cao đỉnh-trũng) trung bình
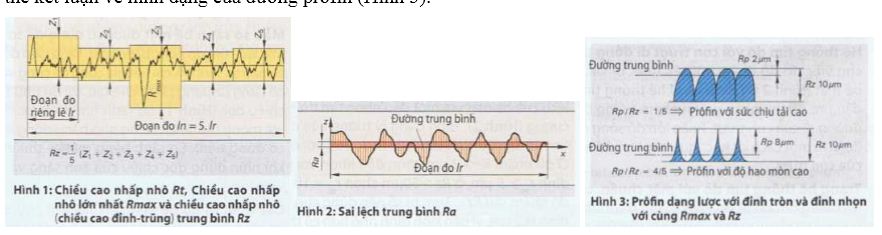
Rzdin là trung bình cộng của từng chiều cao nhấp nhô Z1 đến Z5.
Chiều cao nhấp nhô lớn nhất Rmax là Chiều cao nhấp nhô lớn nhất của 5 lần đo khác nhau.
Chiều cao nhấp nhô Rt là khoảng cách giữa đỉnh cao nhất của đường profin và thung lũng (điểm trũng) thấp nhất của đường prôfin trong tất cả khoảng đo In (Hình 1). Sai lệch trung bình Ra (Trung bình sai lệch số học biên độ) là số trung bình cộng của tất cả trị số tuyệt đối ở trục z của prôtìn nhám trong từng khoảng đo Ir. Ra tương ứng với chiều cao của một hình chữ nhật có diện tích bằng diện tích giữa prôfin và đường trung bình (Hình 2). Các thông số nhám theo quy ước chỉ là độ iớn theo chiều thẳng góc chứ tự nó không nói lên được hình dạng của profin. Qua việc tạo thành tỷ lệ, thí dụ như Rp (độ sâu san phẳng) với Rz người ta cũng có thể kết luận về hình dạng của đường prôfin (Hình 3).
■Các thông số của biểu đồ hiển thị phần vật liệu (biểu đồ Abbott)*
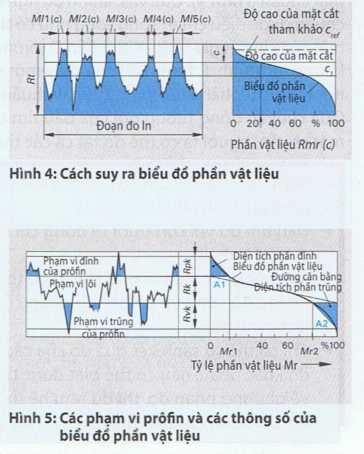
Ta nhận được biểu đồ Abbott, khi trị số phần vật liệu được tìm nhiều như có thể ở nhiều mặt cắt của prôfin bề mặt. ở mỗi đường cắt, ta cộng lại các đoạn cắt đường prôfin và chia tổng sổ với đoạn đường đo. Từ đó phần vật liệu cho ra được tính bằng phần trăm, thí dụ Rmr =25 % ở độ cao đường cắt c1 (Hình 4).
Đường biểu diễn phần vật liệu về diễn tiến của prôfin cho ra lời giải thích về cấu trúc prôfin của bễ mặt. Các thông số dùng để đánh giá các mặt phẳng có chức năng chịu tải cao, thí dụ như của bể mặt trượt.
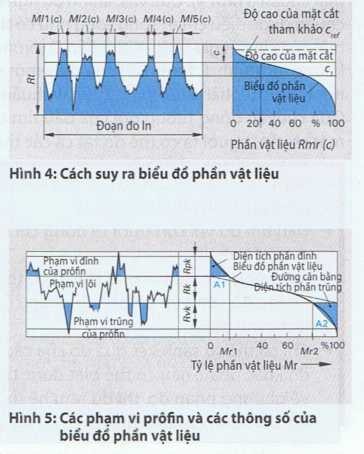
Ta có thể chia biểu đồ phần vật liệu ra làm 3 phạm vi prôfin được qui định bằng các thông số chiều cao đỉnh giản lược Rpk, độ nhám lõi Rk và chiều sâu độ trũng giản lược Rvk. Các độ lớn trung tâm Mr1 và Mr2 cho biết phần vật liệu ở ranh giới của phạm vi lõi (Hình 5).
* được gọi theo tên người Mỹ Abbott.
Những phương pháp kiểm tra bề mặt
Các loại phương pháp kiểm tra Mấu so sánh bề mặt được sử dụng để so sánh bề mặt qua tìm dò hoặc bằng mắt. Điều kiện để so sánh là mẫu so sánh và chi tiết gia công có cùng vật liệu và có cùng phương pháp chế tạo, thí dụ nhưtiện theo chiều dọc (Hình 1). So sánh tìm dò được thực hiện với móng tay hoặc miếng nhỏ bằng đồng (lớn bằng cỡ đồng tiền). So sánh bằng mắt sẽ thuận lợi hơn khi nhìn đúng góc chiếu của ánh sáng và sử dụng kính lúp.
Các thiết bị đo bề mặt làm việc với phương pháp đo biên dạng (phương pháp cắt tìm dò) ghi lại sự sai lệch của bề mặt với một đầu nhọn tìm dò bằng kim cương (Hình 2). Hình dáng lý tưởng của đầu nhọn tìm dò là một hình côn (60° hoặc 90°) với đỉnh tròn, ở độ nhám Rz > 3 um chọn đầu nhọn với bán kính đỉnh r = 5 µm, ở Rz > 50µm chọn r =10µm. Cho độ nham sâu Rz< 3µm trị số nên dùng cho bán kính đỉnh là 2 um, vì bán kính đỉnh nhõ hơn có thể tìm dò tốt hơn ở các thung lũng (điểm trũng) nhỏ của profin. Hệ thống tìm dò với con trượt di động thích hợp cho việc đo độ nhám với các thiết bị xách tay đo bề mặt (Hình 2 và Hình 3). ở hệ thống tìm dò này đầu tìm dò thu nhận prôfin nhám tương đối so với đường đi của con trượt. Phần lớn độ sóng được “lọc (loại) ra một cách cơ học” qua bán kính bằng 25 mm của con trượt.
Trong hệ thống tìm dò với mật chuẩn, còn gọi làhệ thống tìm dò tự do, một thanh trượt (thanh dẫn hướng) rất chính xác trong thiết bị dẫn tiến tạo thành mặt chuẩn (Hình 4). Qua việc chỉnh độ nghiêng, mặt chuẩn được điểu chỉnh song song như có thể với bề mặt của chi tiết gia công. Khi prôfin D (prôfin sơ cấp) không lọc (hình 1, trang 39) cho thấy một vị trí quá nghiêng, thì phải điều chỉnh lại mặt chuẩn tốt hơn. Qua chuyển động tương đối của đầu tìm dò so với mặt chuẩn, người ta có thể đo tất cả các thông số.
Bán kính của đầu tìm dò hạn chế khả năng tìm dò ở các rãnh rất nhỏ
Đầu tìm dò với con trượt di động chỉ nắm bắt được độ nhám.
Hệ thống tìm dò với mặt chuẩn có thể đo độ nhám, độ sóng và các thành phần của sự sai lệch hình dạng.
Chỉ có thể so sánh kết quả đo của các thiết bị đo khác nhau, nếu có thể biết được thông tin về phương pháp đo, thí dụ như hệ thống tìm dò, bán kính của đầu dò và bộ lọc prôfin.
- Phép đo các thông số độ nhám
Các phép đo phải được thực hiện ở vị trí bề mặt nơi được chờ đợi (dự đoán) là có trị số đo xấu nhất, ở prôfin tuần hoàn (có chu kỳ lập lại), thí dụ prôfin của chi tiết tiện thì phải chọn hướng tìm dò thẳng góc với chiều của những đường rãnh, ở prôfin không có tính chu kỳ nơi những đường rãnh thay chiều, chẳng hạn như từ các phương pháp gia công như mài, phay mặt phẳng đầu hoặc miết thì hướng tìm dò sẽ là bất kỳ.
Cách tiến hành ở prôfin tuần hoàn
- Đường rãnh trung bình RSm được ước đoán qua so sánh bằng mắt và tìm dò hoặc tìm qua phép đo thử. ở vận tốc dẫn tiến khi tiện nó tương đương với RSm
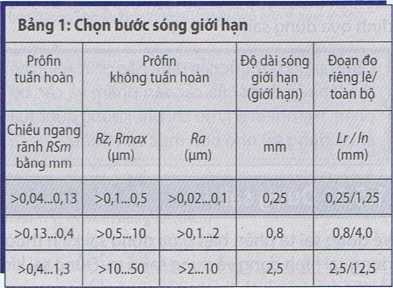
- Từ RSm chọn bước sóng giới hạn λc(cut-off) theo đúng chuẩn và thực hiện phép đo, thí dụ độ nhám trung bình Rz (Bảng 1).
Với sự lựa chọn bước sóng giới hạn thì đoạn đo riêng lẻ cũng được phân bố đúng ở máy đo một cách tự động. Người ta cũng sử dụng cách viết Lc thay cho A.
Cách tiến hành ờ prôfìn không tuần hoàn
- Trị sổ chưa biết Ra hoặc Rz được ước đoán qua so sánh bằng mắt và tìm dò hoặc xét nghiệm qua phép đo thử với độ nhám giả định.
- Phép đo được thực hiện qua sử dụng trị số ước đoán của Ra và Rz với bước sóng giới hạn tương ứng.
Khi trị số đo Ra hoặc Rz không nằm trong phạm vi dự kiến, phép đo phải được thực hiện lại với bước sóng giới hạn lớn hơn hoặc nhỏ hơn (Bảng 1).
Thí dụ:Trị số đã được đo Ra = 1,5 um quá nhỏ so với bước sóng giới hạn 2,5 mm. Phép đo phải được làm lại với bước sóng giới hạn nhỏ hơn là 0,8 mm. Nếu sau đó trị số đo Ra nằm giữa 0,1 µm và 2 µm, như vậy là trị số đo đúng.
Bề mặt có dạng hình núi nên được đo bằng hệ thống tìm dò với mặt chuẩn và với bước sóng giới hạn là 0,8 mm (Hình 1).
Trị số giới hạn trên của độ nhám xem như giữ được, khi trị số đo đầu tiên không vượt quá 70% hoặc 3 trị số đầu tiên không vượt qua trị số giới hạn.