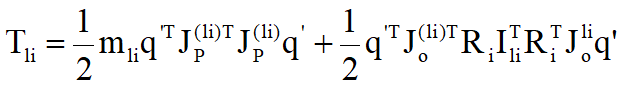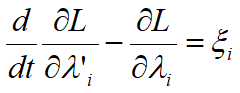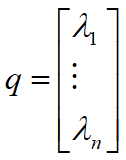Động lực học tay máy
Động lực học tay máy nghiên cứu mối quan hệ giữa lực, mômen, năng lượng… với các thông số chuyển động của nó. Nghiên cứu động lực học tay máy nhằm các mục đích sau:
–Mô phỏng hoạt động của tay máy, để khảo sát, thử nghiệm quá trình làm việc của nó mà không phải dùng tay máy thật.
–Phân tích tính toán kết cấu của tay máy.
Phân tích thiết kế hệ thống điều khiển của tay máy.
- Phương pháp Lagrange:
- 3.1.1. Cơ sở toán học:
- Phương pháp Lagrange dựa trên mối quan hệ giữa tổng năng lượng của hệ thống với lực tổng quát trong một hệ tọa độ tổng quát.
- Giả sử xác định một tập hợp các biến λ với i = 1…n, với tư cách là các thông số mô tả vị trí các khâu của một tay máy có n bậc tự do, hàm lagrange của cơ hệ là hàm số tổng quát của các biến nói trên:
- L = T – U
- Trong đó T và U tương ứng là động năng và thế năng của hệ thống.
Công thức Lagrange được viết như sau:
với i = 1…n
Trong đó š là lực tổng quát liên kết với các tọa độ tổng quát λ
Đối với các tay máy có cấu trúc dạng chuỗi động hở, chọn các tọa độ tổng quát là véc tơ các biến khớp (khớp quay là góc quay, khớp tịnh tiến là lượng tịnh tiến):
Lực tổng quát có thể bao gồm mô men phát động trên trục động cơ, mômen ma sát tại cácổ trục, lực tương tác giữa phần công tác với đối tượng….
Ví dụ 1:
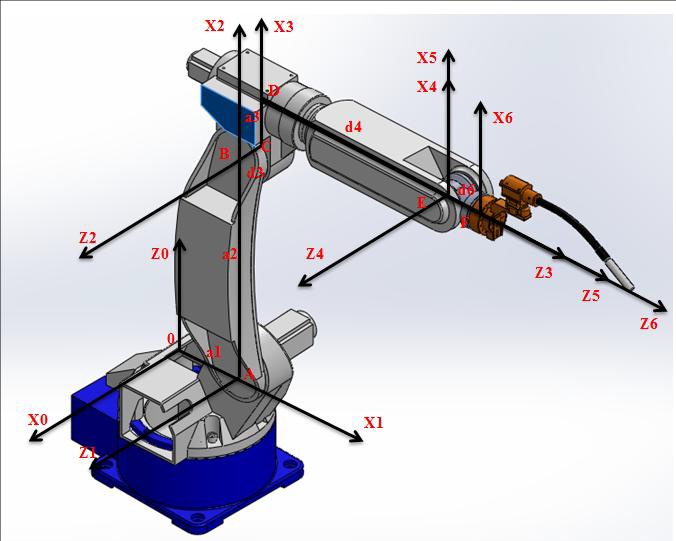
Mô hình động học của trục dao động tượng trưng cho một khâu chuyển động quay tròn của robot, được dẫn động bởi một động cơ độc lập như hình vẽ: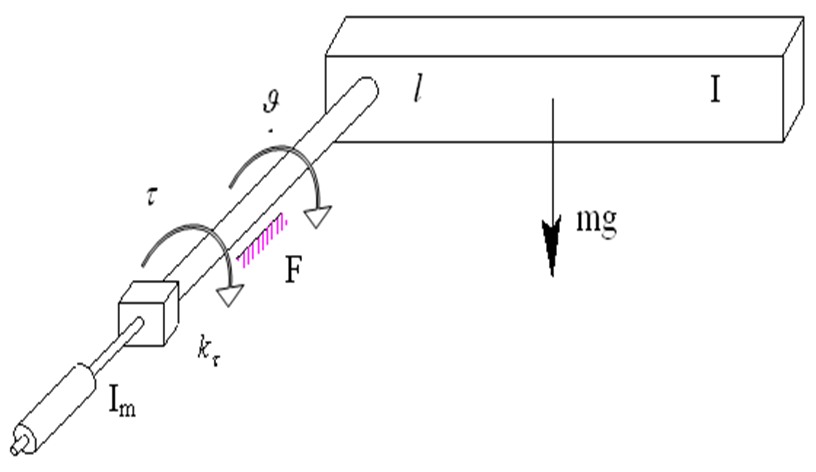 
Trên hình vẽ động cơ điện có có mômen quán tính Im , nối với hộp giảm tốc có tỉ số truyền kr , nhờ đó, trục được truyền một mô men chủ động và có vận tốc góc . Vật quay có khối lượng m, mômen quán tính I và tọa độ trọng tâm đặt cách trục dẫn động một khoảng l. Chọn thông số chính mô tả vị trí của trục quay là góc quay của trục (xem hình vẽ). Có nghĩa là tính ngược lại qua tỉ số truyền của hộp giảm tốc trục động cơ phải quay một góc . Khi đó động năng của hệ thống tính theo công thức: 
- Phương trình này có ý nghĩa như sau:
Để quay trục chấp hành đi một góc 
cần tác dụng lên trục động cơ một lực tối thiểu π , lực này dùng tạo ra tất cả các thành phần có công âm ở vế trái, trong đó:
–Các đại lượng gắn với ” trong phương trình mô tả hiệu ứng của lực quán tính (đạo hàm bậc hai của góc quay là gia tốc góc, gia tốc góc gắn với lực quán tính).
–Các đại lượng gắn với ‘trong phương trình mô tả hiệu ứng tương hỗ (đạo hàm bậc nhất của góc quay là vận tốc, vận tốc lũy thừa một gắn với lực ma sát).
–Các đại lượng gắn với ‘2 trong phương trình mô tả hiệu ứng li tâm (trong ví dụ này bỏ qua hiệu ứng li tâm nên không có mặt thừa số này).
Các đại lượng gắn với trong phương trình mô tả hiệu ứng trọng lực (lực trọng trường).
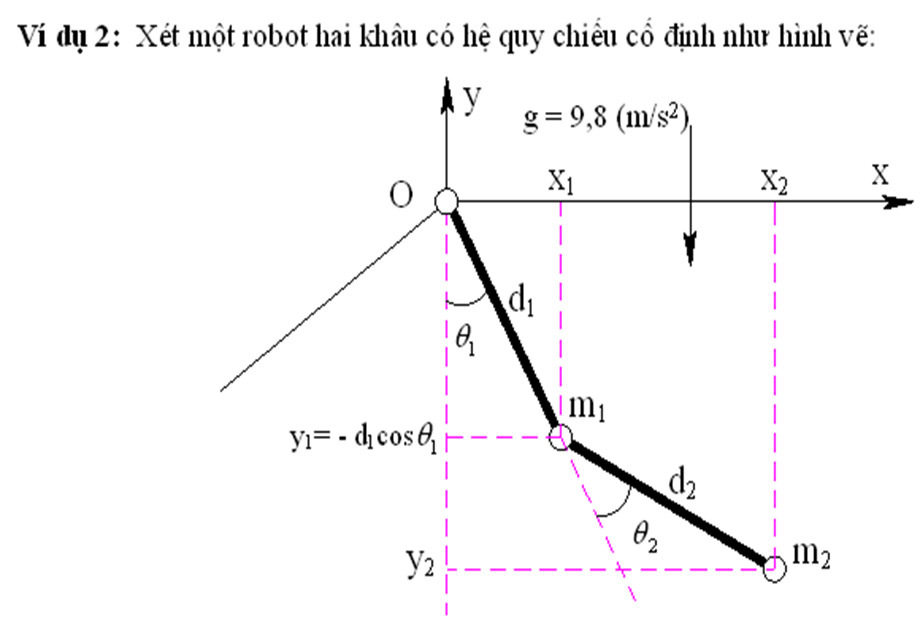
Hai khâu của robot có chiều dài d1; d2 với các khối lượng tương ứng m1; m2. Các khớp quay hoạt động với biến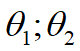 
hãy xác định biểu thức tính lực tổng quát.
- Với khâu 1:
-
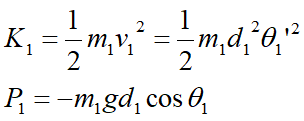
- Trong đó K kí hiệu của động năng, ở đây chỉ xét động năng của khâu mà không kể động cơ, P là thế năng của khâu
- Khâu 2 chuyển động theo phương trục x và trục y đồng thời nên vận tốc tổng hợp bằng đường chéo hình chữ nhật tính theo pitago như sau:
ĐỘNG NĂNG
Sơ đồ tính động năng chuyển động
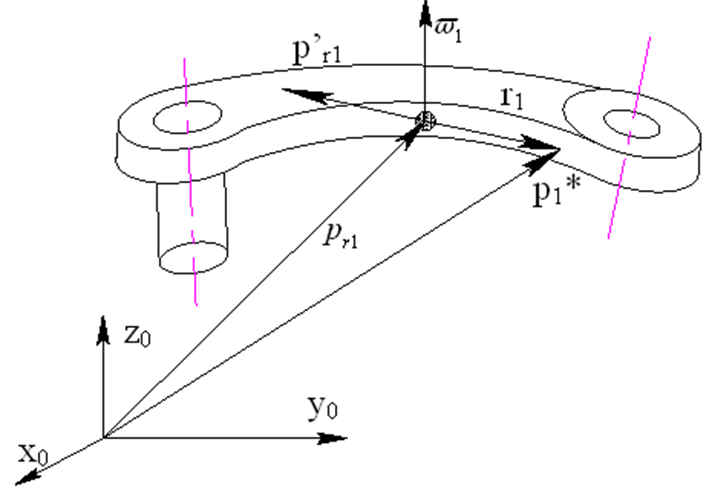
- Động năng của hệ thống gồm hai phần là động năng của phần chấp hành và động năng của cơ cấu phát động cùng với hệ thống truyền động:
- Động năng chuyển động Tli có thể được tính theo sơ đồ ở trên:
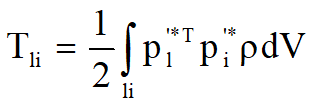
- Trong đó
-
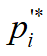là vector vận tốc dài (v2 = p’*iT.p’*i) - P là khối lượng riêng của phân tố thể tích dV
- Vli là thể tích của khâu thứ i:
-
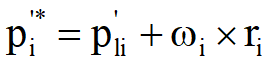
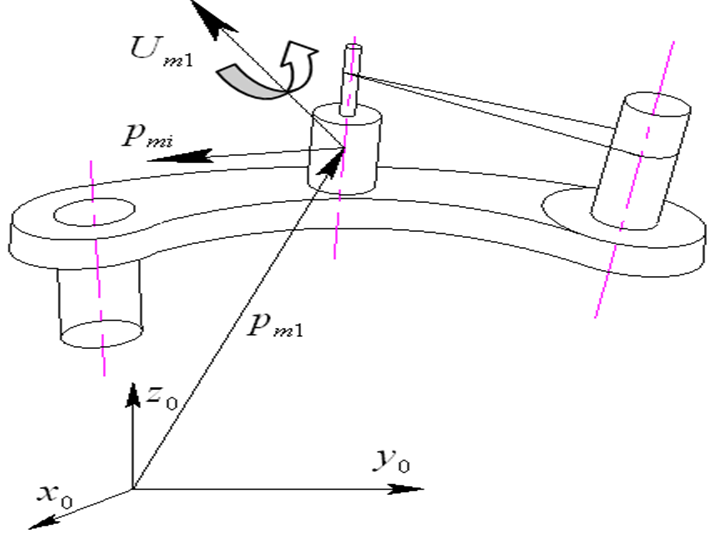
- Sơ đồ tính động năng khâu dẫn
