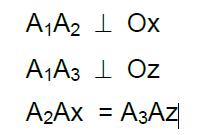Hình chiếu của điểm
Trên hai mặt phẳng hình chiêu.
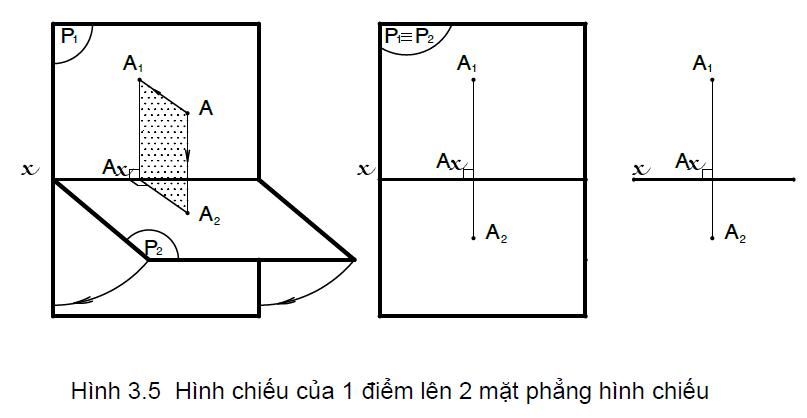
Trong không gian, lấy hai mặt phẳng P1 và P2 vuông góc với nhau (mặt phẳng P1 đặt thẳng đứng , mặt phẳng P2 đặt nằm ngang ). Từ một điểm A bất kỳ trong không gian, dựng đường vuông góc với P1 và P2. Ta có A1 trên P1 và A2 trên P2 .
Điểm A1 được gọi là hình chiếu đứng và điểm A2 là hình chiếu bằng của điểm A (hình 3.5).
Để vẽ hai hình chiếu của điểm A trên cùng một mặt phẳng, ta xoay P2 quanh trục x một góc 90°( theo chiều qui ước ) về trùng mặt phẳng P1. Cặp điểm (A1,A2) nằm trên đường vuông góc với trục x còn gọi là đồ thức của điểm A. Để đơn giản chỉ vẽ trục x và cặp hình chiếu A1,A2.
Ngược lại, có cặp điểm ( A1,A2 ) ta có thể xác định được điểm A trong không gian bằng cách xoay P2 trở lại vị trí nằm ngang, dựng các đường vuông góc từ A2 lên và từ A1 ra, hai đường này sẽ cắt nhau tại A.
Trên ba mặt phẳng hình chiếu
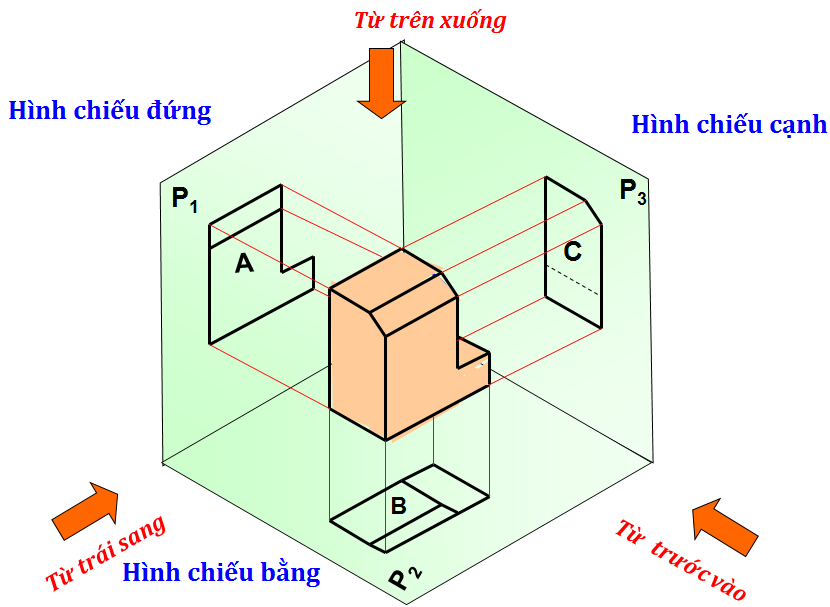
Lần lượt chiếu điểm A lên 3 mặt phẳng hình chiếu, tương tự ta có A3 là hình chiếu cạnh của điểm A. Sau khi xoay P2 như trên, ta xoay P3 quanh trục z về phía bên phải của P1. Ta có 3 hình chiếu A1, A2, A3 cùng nằm trên một mặt phẳng bản vẽ P1≡ P2 ≡ P3(hình 3.6a). Chúng mang tính chất sau:
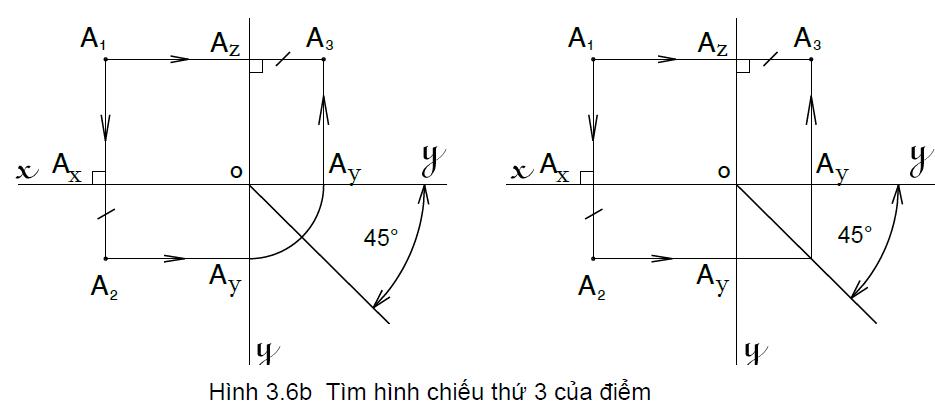
Dựa vào tính chất này, bao giờ ta cũng xác định được hình chiếu thứ ba khi biết được hai hình chiếu vuông góc của điểm (hình 3.6b).
Hình chiếu của một đường thẳng
Một đường thẳng được xác định khi ta biết hai điểm không trùng nhau. Do đó, muốn vẽ hình chiếu vuông góc của đường thẳng hay đoạn thẳng, ta chỉ cần vẽ hình chiếu vuông góc của hai điểm đó rồi nối chúng lại.
Thực tế, đường thẳng thường thể hiện dưới dạng đoạn thẳng nên chủ yếu ta chỉ xét hình chiếu của đoạn thẳng.
Hình chiếu của đoạn thẳng trên một mặt phẳng hình chiếu
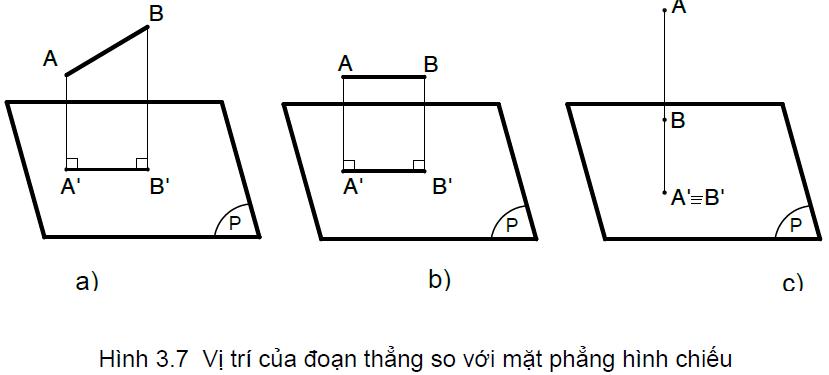
Tùy theo vị trí của đoạn thẳng so với mặt phẳng hình chiếu, ta có 3 trường hợp :
– Đoạn thẳng xiên với mặt phẳng hình chiếu: hình chiếu của nó là đoạn thẳng không song song và có độ dài không bằng nó ( A’B'< AB) (hình 3.7a).
– Đoạn thẳng song song với mặt phẳng hình chiếu: hình chiếu của nó là đoạn thẳng song song và có độ dài bằng nó ( A’B’= AB) (hình 3.7b).
– Đoạn thẳng vuông góc với mặt phẳng hình chiếu: hình chiếu của nó là một điểm (A’B’) (hình 3.7c).
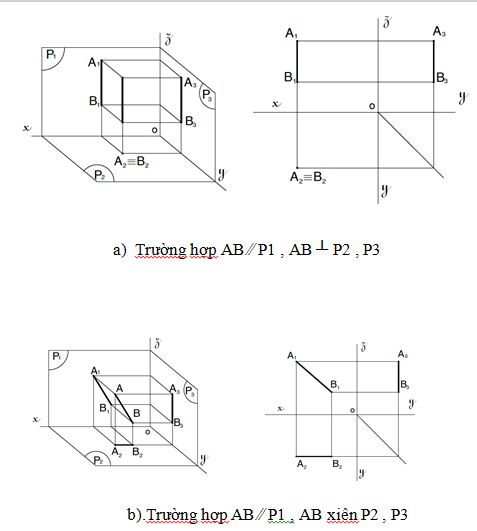
Hình chiếu của đoạn thẳng trên ba mặt phẳng hình chiếu
_Để tìm hình chiếu của đoạn thẳng trên 3 mặt phẳng hình chiếu, ta xem vị trí đoạn thẳng so với từng mặt phẳng hình chiếu rồi lần lượt chiếu nó lên các mặt phẳng hình chiếu đó. Sau đó, xoay các mặt phẳng hình chiếu theo qui ước về trùng một mặt phẳng bản vẽ, ta có 3 hình chiếu của đoạn thẳng trên một mặt phẳng bản vẽ (hình 3.8).
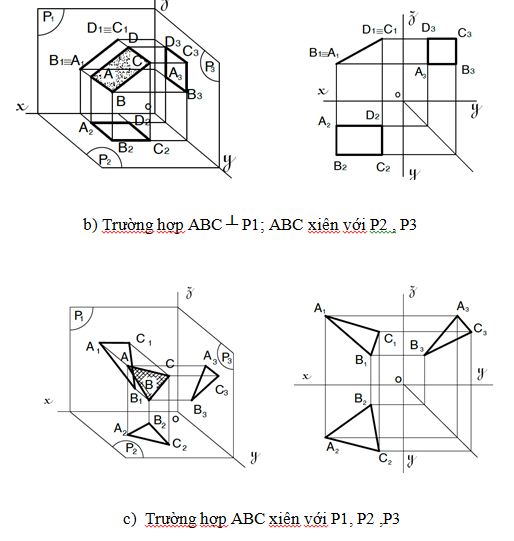
Hình chiếu của hình phẳng lên 3 mặt phẳng hình chiếu
_Muốn tìm hình chiếu của hình phẳng trên 3 mặt phẳng hình chiếu, ta xem vị trí hình phẳng so với từng mặt phẳng hình chiếu rồi lần lượt chiếu nó lên các mặt phẳng hình chiếu đó. Sau đó xoay các mặt phẳng hình chiếu theo qui ước về trùng một mặt phẳng bản vẽ, ta có 3 hình chiếu của hình phẳng trên mặt phẳng bản vẽ