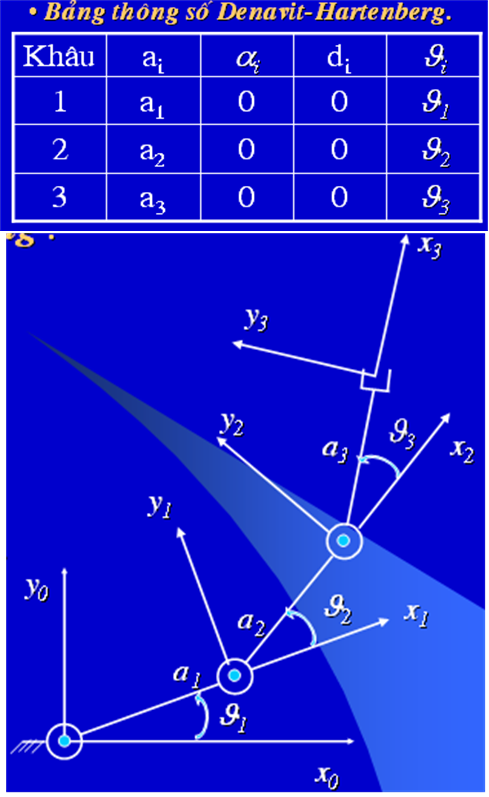
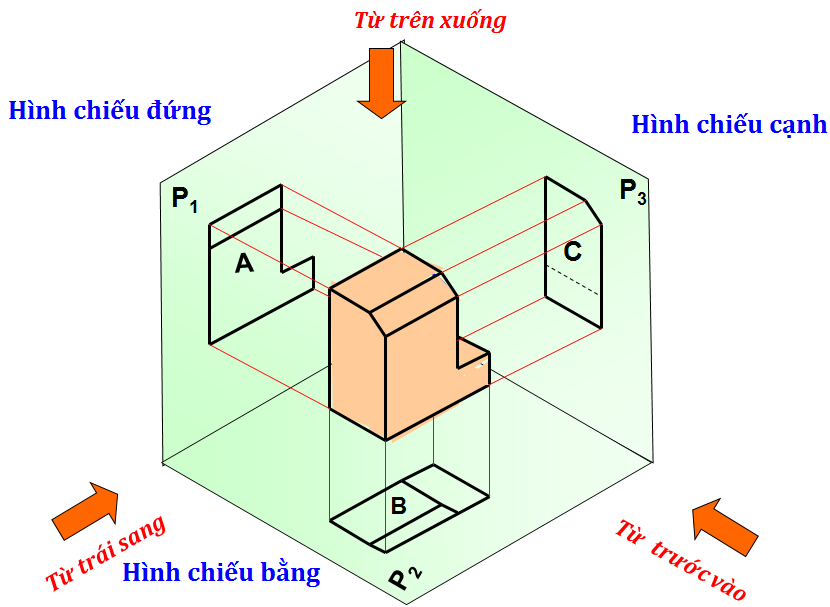
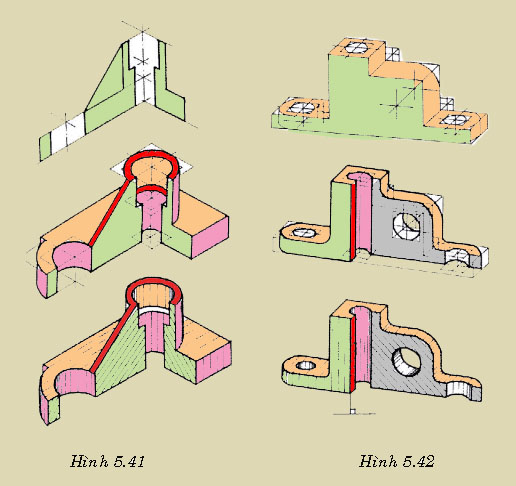
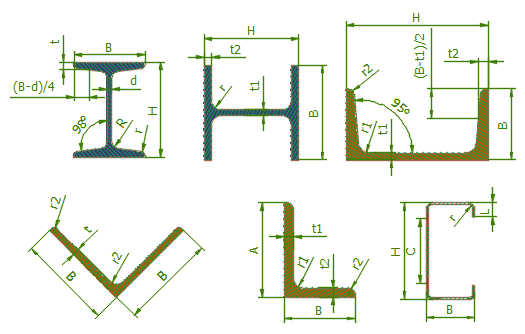
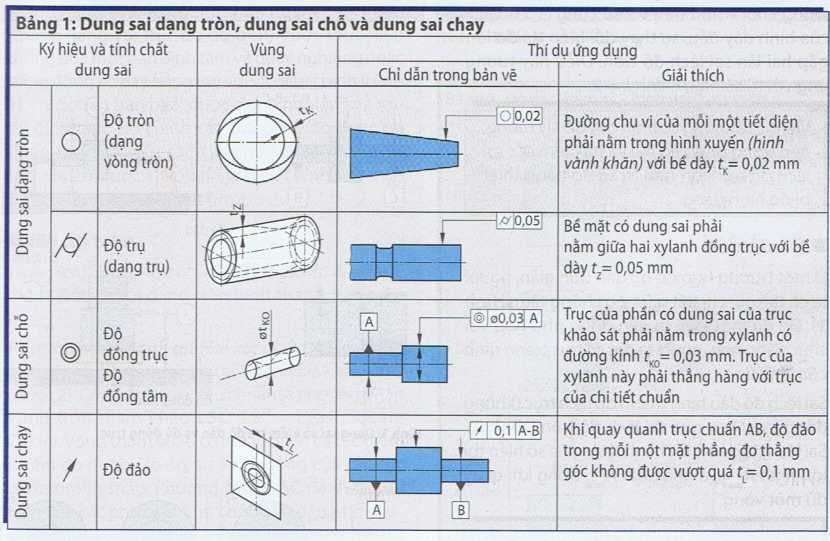
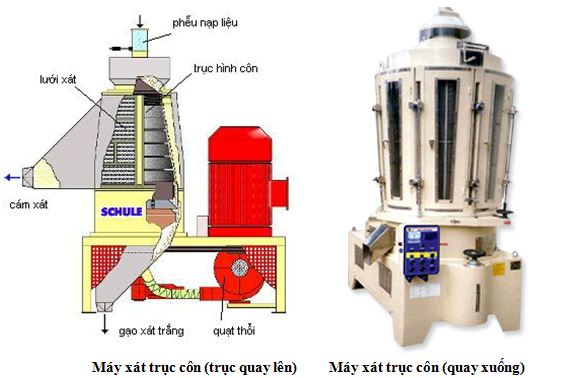
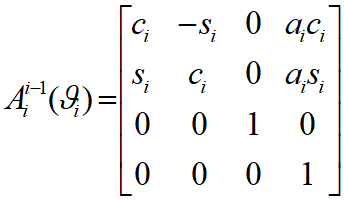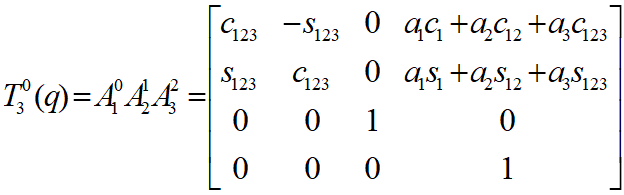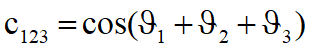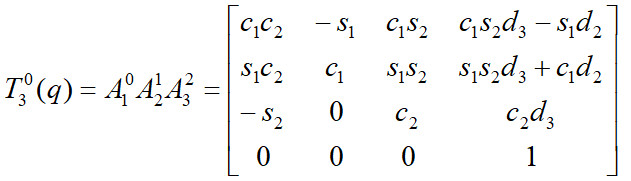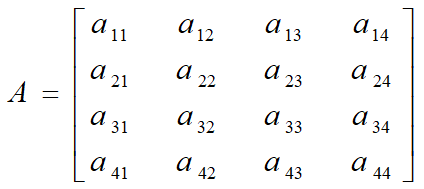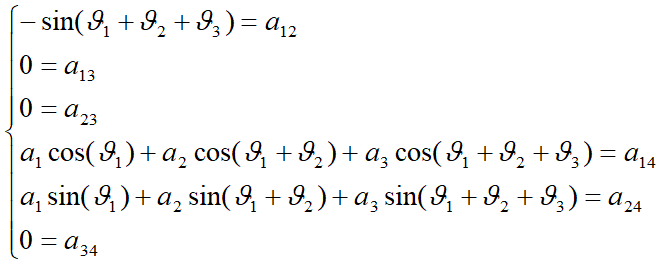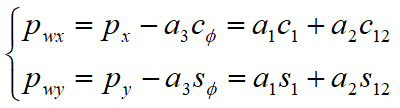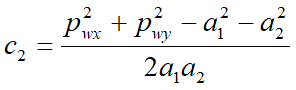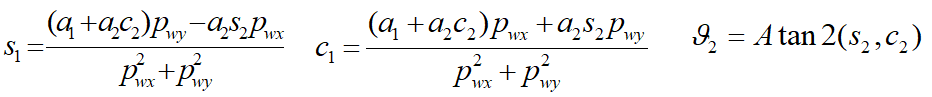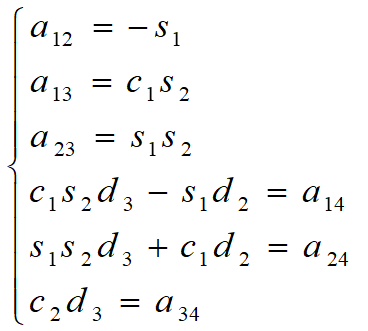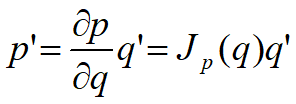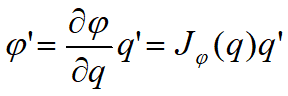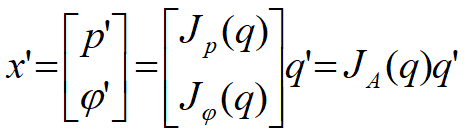Robot công nghiệp_Bài 4: ứng dụng quy tắc Dẫn Hướng

Một số ví dụ ứng dụng quy tắc DH:

Tay máy ba khâu phẳng:

Sơ đồ động học của tay máy cho thấy như hình vẽ:

Thay các thông số tương ứng vào các ma trận mẫu tổng quát nói trên nhận được ma trận biến hình cho từng bước như sau:

Khi nhân các ma trận này với nhau có ma trận chuyển đổi tổng hợp:

Ở đây kí hiệu:

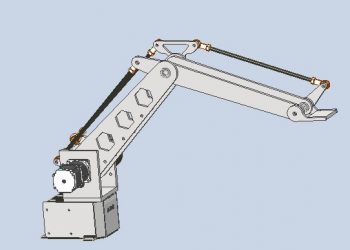
Tay máy tọa độ cầu:

Sơ đồ động và bảng thông số DH cho thấy như hình vẽ:

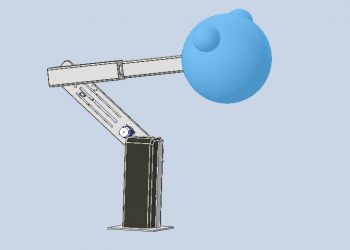
Vùng hoạt động của phần công tác:

Tập hợp các điểm mà tay máy có khả năng định vị và định hướng phần công tác thỏa mãn yêu cầu công việc tạo thành một hoặc vài miền liên tục, miền đó được gọi là miền công tác, hay vùng làm việc, Những điểm thuộc vào vùng làm việc mà tay máy không thể đạt được định vị ở đó do các lí do kết cấu gọi là lỗ trống.
Vùng làm việc của tay máy là một thông số quan trọng của nó, thể tích và hình dạng của vùng làm việc phụ thuộc vào kết cấu của tay máy và giới hạn của các biến khớp.

Đôi khi người ta có phân biệt vùng với tới và vùng với tới có định hướng, để biểu diễn được vùng làm việc, xác định phần với tới có đinh hướng và với tới không định hướng cần có các kĩ năng toán học, và trên cơ sở đặc điểm cụ thể của từng loại tay máy.

. Bài toán động học ngược của tay máy:

Bài toán thuận động học nhằm xác định định vị và định hướng của phần công tác khi cho trước các biến khớp. Bài toán ngược cho trước vị trí và định hướng của khâu tác động sau cùng đòi hỏi phải xác định bộ thông số tọa độ suy rộng để đảm bảo chuyển động cho trước của phần công tác.
Đối với tay máy có kết cấu dạng chuỗi động hở, nếu cho trước bộ thông số biến khớp thì vị trí và định hướng của phần công tác xác định duy nhất, điều này không đúng với các tay máy có cấu trúc dạng chuỗi động kín.

Đối với các tay máy dạng chuỗi động hở, ứng với một bộ thông số mô tả định vị và định hướng của phần công tác khi giải bài toán ngược có thể xảy ra các trường hợp:

–Có thể có nhiều lời giải khác nhau;

–Các phương trình đồng nhất thức thường có dạng phi tuyến, siêu việt, thường không cho lời giải đúng;

–Có thể gặp nghiệm vô định vì có các liên kết thừa giống kiểu kết cấu siêu tĩnh;

Có thể có lời giải toán học, song lời giải này không chấp nhận được về mặt vật lí do các yếu tố về kết cấu của cấu trúc không đáp ứng được.

Nhìn chung khi số bậc tự do càng lớn thì bài toán ngược càng khó giải, số nghiệm toán học lại càng nhiều, khi đó để chọn được nghiệm điều khiển đòi hỏi phải loại bỏ các nghiệm không phù hợp dựa trên cơ sở các ràng buộc về giới hạn hoạt động của các khớp. Việc lựa chọn phương pháp để giải bài toán ngược cũng là một vấn đề, cho đến nay không có phương pháp tổng quát nào có thể áp dụng cho tất cả các robot. Sau đây giới thiệu một số ví dụ bài toán ngược tay máy của các cơ cấu đã giải bài toán thuận ở mục trước.

Cơ cấu ba khâu phẳng:

Dựa trên kết quả đã triển khai ở bài toán thuận, ta đã có phương trình động học của tay máy này dưới dạng ma trận đồng nhất (4.4):

Ma trận định vị và định hướng phần tác động sau cùng trên cánh tay được cho trước trong bài toán ngược dưới dạng như sau:

Nhiệm vụ của bài toán ngược phải xác định một bộ công thức tính dựa trên các đồng nhất thức tạo ra từ hai ma trận trên.

Vì biến số nằm trong góc nên nếu giải trực tiếp hệ phương trình mô tả định vị và định hướng là không thể. Hãy xem hệ thiết lập được trên 2 điều kiện này:

Ba phương trình đầu của hệ mô tả định hướng của khâu sau cùng, ba phương trình sau mô tả định vị của khâu sau cùng. Vì hệ suy biến nên thực chất còn ba phương trình, ba ẩn:

Nếu đặt 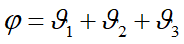, để mô tả định hướng của khâu sau cùng, phải cho trước giá trị này.
Vậy nếu xem đây là hệ hai phương trình hai ẩn với 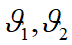Matlab có thể giải ra kết quả, từ đó tính ra tuy nhiên kết quả rất dài không có tính thực tế.

Nếu coi điểm W là tâm của khớp quay thứ ba, hay là điểm tựa công nghệ. Định hướng của khâu sau cùng sẽ đạt được trên cơ sở xoay hướng khâu sau cùng phải là φ từ điểm này.

Điểm tựa công nghệ W có thể xác định bằng hình học như sau:

Bình phương hai vế phương trình này rồi cộng lại nhận được:

C2 phải thỏa mãn miền giá trị của hàm cosin. Tính được:

Thay c2 vào hệ phương trình trên và giải ra được:

Cuối cùng tính được: J3 = f – J1 – J2

Bài toán ngược kết thúc phần xác định nghiệm toán học, cần tiếp tục căn cứ vào các yêu cầu cụ thể chọn nghiệm điều khiển.

Cơ cấu cầu:

Phương trình động học cơ cấu cầu đã xác định trong bài toán thuận, nếu tổng quát bài toán ngược đòi hỏi đáp ứng cả định vị và định hướng của điểm quản lí, sẽ phải giải hệ 6 phương trình (ba định vị, ba định hướng) để xác định các biến khớp .

Xuất phát từ phương trình động học trong bài toán thuận:

Ma trận mô tả định vị, định hướng của phần công tác biết trước:

Hệ 6 phương trình ba ẩn như sau:

Chúng ta thấy ba phương trình đầu mô tả định hướng của phần làm việc vì vậy không liên quan gì đến tầm với d3, mà chủ yếu liên quan đến hai bậc tự do quay. Ngược lại, ba phương trình sau mô tả định vị nên liên quan chặt chẽ đến tầm với d3.

Nếu không đòi hỏi định hướng, chỉ xét hệ gồm ba phương trình sau trong hệ

Bài toán vận tốc:

Bài toán vận tốc có thể giải theo hai cách, dựa trên quan hệ hình học hoặc dựa trên quan hệ giải tích. Ở đây trình bày lời giải theo quan hệ giải tích (vi phân động học) để có thể kế thừa được các kết quả của phần tính toán động học nói trên.
Biết rằng chuyển vị là lời giải của bài toán ngược động học, còn đạo hàm bậc nhất của chuyển vị theo thời gian chính là vận tốc. Hãy xem quan hệ sau:

– Vận tốc chuyển động tịnh tiến của phần công tác so với hệ cơ sở được tính bằng cách lấy đạo hàm của tọa độ p(q) theo thời gian: