1/ Cách dựng hình
1.1/ Dựng đường thẳng song song, đường thẳng vuông góc, dựng và chia góc
a. Dựng đường thẳng song song
b. Dựng đường thẳng vuông góc.
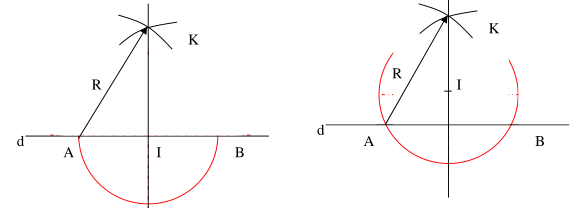
Dựng đường thẳng vuông góc với đường thẳng d đi qua I thuộc d:
- Dựng đường tròn tâm I cắt d tại A và B
- Dựng các cung tròn tâm A và B bán kính R = AB cắt nhau tại K
- Đường thẳng qua K và I sẽ vuông góc với d.
- Dựng đường thẳng vuông góc với đường thẳng d đi qua I không thuộc d
1.2/ Chia đều đoạn thẳng, chia đều đường tròn
a/ Chia đều đoạn thẳng ( Phương pháp tỷ lệ)
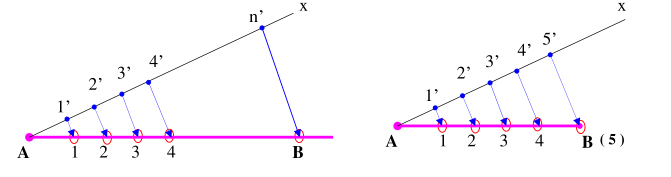
LT: Chia đều đoạn thẳng AB thành nhiều đoạn bằng nhau( n đoạn bằng nhau), cách vẽ như sau:
- Qua điểm A (hoặc B) kẻ dường thẳng Ax bất kỳ ( nên lấy góc xAB là một góc nhọn)
- Kể từ A đăt lên Ax, n đoạn bằng nhau bằng các điểm chia 1’, 2’ , 3’ , 4’…
- Nối n’ B và qua điểm 1’, 2’ , 3’ , 4’… kẻ các đường thẳng song song với n’B . Giao điểm của các đường thẳng đó với AB cho ta các điểm chia tương ứng 1, 2, 3, 4…B, đó là những điểm chia cần tìm
VD: Chia 1 đoạn thẳng ra làm 5 phần bằng nhau. b. Chia đều đường tròn
b/ Chia 3
- Dựng đường tròn tâm O, đường kính AB, bán kính R
- Dựng đường tròn tâm B bán kính R cắt đường tròn tâm O tại 1, 2
- Ba điểm A, 1, 2 chia đều đường tròn tâm O thành 3 phần bằng nhau.
c/ Chia 4
- Dựng đường tròn tâm O,
- Dựng đường kính AB, bán kính R
- Dựng đường vuông góc với AB qua O cắt đường tròn tâm O tại 1, 2
- Bốn điểm 1, B, 2,A chia đều đường tròn tâm O thành 4 phần bằng nhau.
d/ Chia 5
Ta chia đường tròn ra 5 phần bằng nhau bằng cách d−ụng độ dài của cạnh hình 5 cạnh đều nội tiếp trong đường tròn đó. Theo công thức: a5= r/2.
- Dựng đường tròn tâm O, đường kính AB, bán kính R
- Qua tâm O dựng 2 đường kính AB, CD vuông góc với nhau
- Lấy trung điểm M của đoạn OA
- Lấy M làm tâm kẻ cung tròn bán kính MC, cung này cắt OB ở N , ta có CN là độ dài cạnh a5= r/2 của hình 5 cạnh đều nội tiếp trong đường tròn đó.
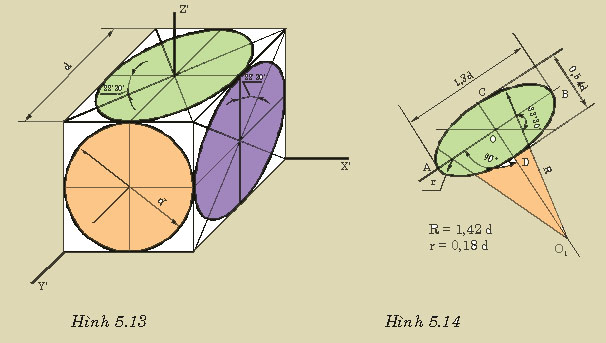
1.2/ Sử dụng phép chiếu xuyên tâm
a/ Sử dụng phép chiếu xuyên tâm khi dựng hình
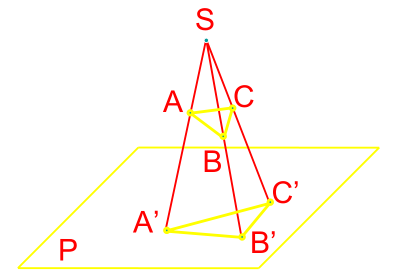
Trong không gian, lấy mặt phẳng P và một điểm S nằm ngoài P Từ một điểm A bất kỳ trong không gian, dựng đường thẳng S A, đường này cắt P tại điểm A’. Ta đã thực hiện một phép chiếu.
- Mặt phẳng P gọi là mặt phẳng hình chiếu.
- Đường thẳng SA là tia chiếu.
- Điểm A’ gọi là hình chiếu xuyên tâm của điểm A trên mặt phẳng hình chiếu P qua tâm chiếu S.
- Các tia chiếu đều đi qua điểm S cố định.
b/ Phép chiếu xuyên tâm
Khái niệm
Phép chiếu xuyên tâm là một phép chiếu tồn tại hai yếu tố sau đây:
- Mặt phẳng hình chiếu P
- Tồn tại một tâm chiếu S ( S là một điểm không thuộc P )
- Chiếu một điểm A từ tâm S lên mặt phẳng P bằng cách vẽ đường thẳng SA, xác định được điểm A’ là giao điểm của SA với mặt phẳng P, hay hình chiếu A’ là của A trên P.
- Vậy phép chiếu xuyên tâm là một phép chiếu phẳng dụng tâm chiếu S để chiếu vật lên mặt phẳng chiếu.
Tính chất cơ bản của phép chiếu xuyên tâm
- Hình chiếu của một điểm là một điểm. Điểm thuộc mặt phẳng hình chiếu chính là điểm trùng với chính nó. Hình chiếu của một đường thẳng không đi qua tâm chiếu là một đường thẳng.
- Đường thẳng đi qua tâm chiếu gọi là đường thẳng chiếu. Hình chiếu của đường thẳng chiếu là một điểm. Mặt phẳng đi qua tâm chiếu gọi là mặt phẳng chiếu. Hình chiếu của mặt phẳng chiếu là một đường thẳng. Phép chiếu xuyên tâm bảo toàn tỷ số kép của bốn điểm thẳng hàng.
1.3/ Phép chiếu song song
a. Khái niệm
Cho một mặt phẳng ∏ gọi là mặt phẳng hình chiếu, và một đường thẳng I không song song với mặt phẳng ∏ và gọi là hướng chiếu.
Vậy phép chiếu song song của một điểm A lên mặt phẳng ∏ là một điểm A’ được thực hiện bằng cách vạch qua A một đường thẳng song song với đường thẳng I và cắt mặt phẳng ∏ tại một điểm đó chính là A’.
Vậy phép chiếu song song là một trường hợp đặc biệt của phép chiếu xuyên tâm khi tâm chiếu ra xa vô tận.
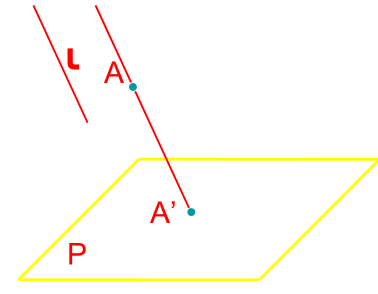
Cho mặt phẳng P và một đường thẳng l không song song với P, từ một điểm A trong không gian ta dựng một đường thẳng song song với l, đường thẳng đó cắt mặt phẳng p tại điểm A’.
Mặt phẳng P gọi là mặt phẳng hình chiếu.
Đường thẳng cố định l gọi là phơng chiếu.
A’ gọi là hình chiếu song song của điểm A trên mặt phẳng hình chiếu P.
Tính chất:
- Có đầy đủ tính chất của phép chiếu xuyên tâm
- Hình chiếu song song của các đường thẳng song song là các đường thẳng song song
VD: cho hai đường thẳng AB // CD dùng phép chiếu song song lên mặt phẳng ∏ ta được hai đường thẳng mới A’B’ và C’D’ theo tính chất trên thì A’B’ // C’D’ - Tỷ số của hai đường thẳng song song qua phép chiếu song song cũng cho tỷ số bằng chính tỷ số đó
VD: cho hai đường thẳng AB // CD dùng phép chiếu song song lên mặt phẳng ∏ ta được hai đường thẳng mới A’B’ và C’D’ theo tính chất trên thì AB/CD = A’B’/C’D’
1.3/ Phép chiếu vuông góc khi dựng hình
a/ Định nghĩa
Phép chiếu vuông góc là một phép chiếu mà trong đó đường thẳng hướng chiếu I vuông góc với mặt phẳng hình chiếu. ( I vuông góc với ∏ )
Cho mặt phẳng P và một điểm A trong không gian, từ A dựng đường vuông góc với mặt phẳng P, chân đường vuông góc là A’, A’ gọi là hình chiếu vuông góc của điểm A trên mặt phẳng hình chiếu P.
Tính chất
Có đầy đủ tính chất của phép chiếu song song. Độ dài hình chiếu thẳng góc A’B’ của đoạn thẳng AB sau phép chiếu thẳng góc bằng đọ dài AB nhân với cosϕ (ϕ: là góc nghiên của AB so với ∏ ) hay ta có: [A’B’] = [AB.cosϕ]
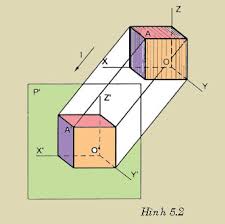
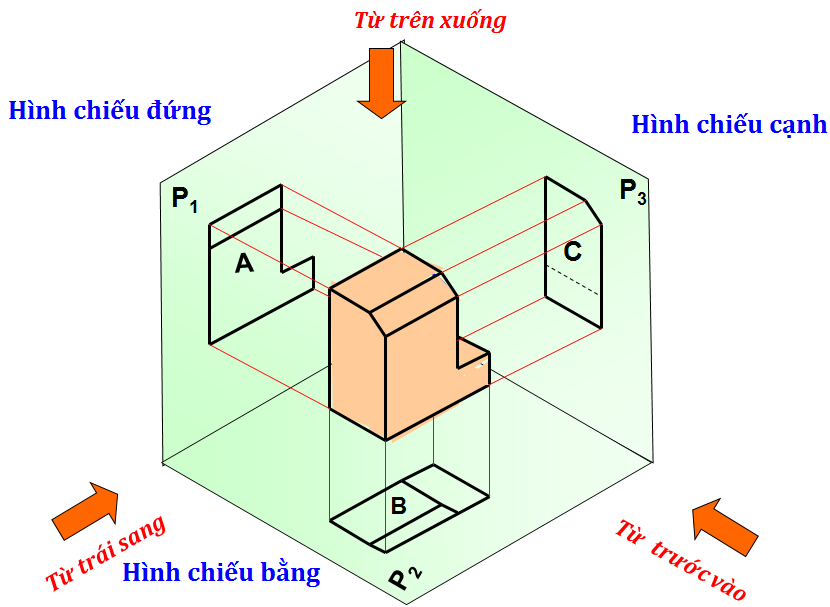
b/ Các mặt phẳng hình chiếu và các trục chiếu a
Định nghĩa các mặt phẳng hình chiếu
Trong vẽ kỹ thuật người ta có ba loại mặt phẳng hình chiếu sau:
- Mặt phẳng hình chiếu bằng( kí hiệu: P 2) là mặt phẳng nằm ngang dùng để thể hiện hình chiếu bằng.
- Mặt phẳng hình chiếu chính ( hình chiếu đứng) ( kí hiệu: P 1 ) là mặt phẳng thẳng đứng, vuông góc với mặt phẳng chiếu bằng, dùng để thể hiện hình chiếu chính của vật thể.
- Mặt phẳng hình chiếu cạnh ( kí hiệu: P 3 ) là mặt phẳng thẳng đứng nhưng vuông góc với hình chiếu chính và chiếu bằng, nó được dùng để thể hiện hình chiếu cạnh của vật thể.
c/ Các trục chiếu
Trong không gian muốn biểu diễn vị trí, hình dạng của một điểm, đường, một mặt, hay vật thể người ta thường sử dụng hệ trục toạ độ không gian ba chiều Oxyz hay còn gọi là trục toạ độ Đề các. gồm ba trục chiếu sau:
- Trục toạ độ Ox, Oy, Oz đây là ba trục chiếu vuông góc với nhau từng đôi một
- Ox là trục hoành hay còn gọi là hoành độ
- Oy là trục tung hay còn gọi là tung độ
- Oz là trục cao hay còn gọi là cao độ.
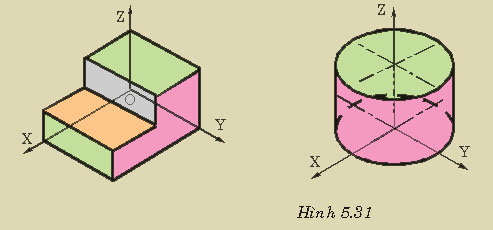
Khi thực hiện phép chiếu song song với trục Oz ta thể hịên được hình chiếu bằng.
Khi thực hiện phép chiếu song song với trục Oy ta thể hiện được hình chiếu cạnh.
Khi thực hiện phép chiếu song song với trục Ox ta thể hiện được hình chiếu đứng.
1.4/ Phép chiếu điểm
a/ Hình chiếu của 1 điểm là một điểm
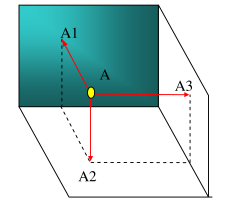
Giả sử có điểm A trong không gian, xây dựng hình chiếu của A của nó như sau:
- AA1 vuông góc với P1, A1 là chân đường vuông góc, thì A1 là hình chiếu đứng của điểm A.
- AA2 vuông góc với P2, A2 là chân đường vuông góc, thì A2 gọi là hình chiếu bằng của điểm A.
- AA3 vuông góc với P3, A3 là chân đường vuông góc, A3 được gọi là hình chiếu cạnh của điểm A.
b/ Để có hình chiếu trên mặt phẳng giấy vẽ, ta xoay P2 và P3 chập lại với P1
– Xoay quanh trục X cho nửa trước P2 xuống dưới chập vào P1.
– Xoay quanh trục Z cho nửa trước P3 sang phải chập vào P1.
>> Vậy ta có ban hình chiếu của A trên cùng một mặt phẳng.
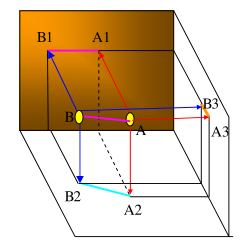
c/ Hình chiếu của đường thẳng
Trong không gian một đường thẳng được giới hạn bởi 2 điểm phân biệt. Vì vậy khi cho hình chiếu của hai điểm ta xác định được hình chiếu của đường thẳng qua hai điểm đó.
- Hình chiếu đứng của đường thẳng là đường nối của hình chiếu đứng của hai điểm đó.
- Hình chiếu bằng của đường thẳng là đường nối hình chiếu bằng của hai điểm.
- Hình chiếu cạnh của đường thẳng là đường thẳng nối hình chiếu cạnh của 2 điểm.
d/ Hình chiếu của mặt phẳng
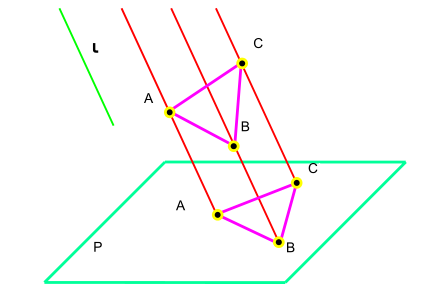
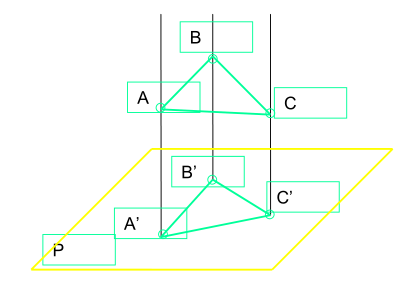
Trong không gian, mặt phẳng có thể được xác định bằng 3 điểm, hoặc hai đường thẳng cắt nhau, hai đường thẳng song song, một đường thẳng và một điểm
>>> Vậy hình chiếu của một mặt phẳng là hình chiếu của các đối tượng được xét ở trên
- Hình chiếu của ba điểm không thẳng hàng.
- Hình chiếu của hai đường thẳng cắt nhau
- Hình chiếu của hai đường thẳng song song
- Hình chiếu của một điểm và một đường