Hình chiếu trục đo

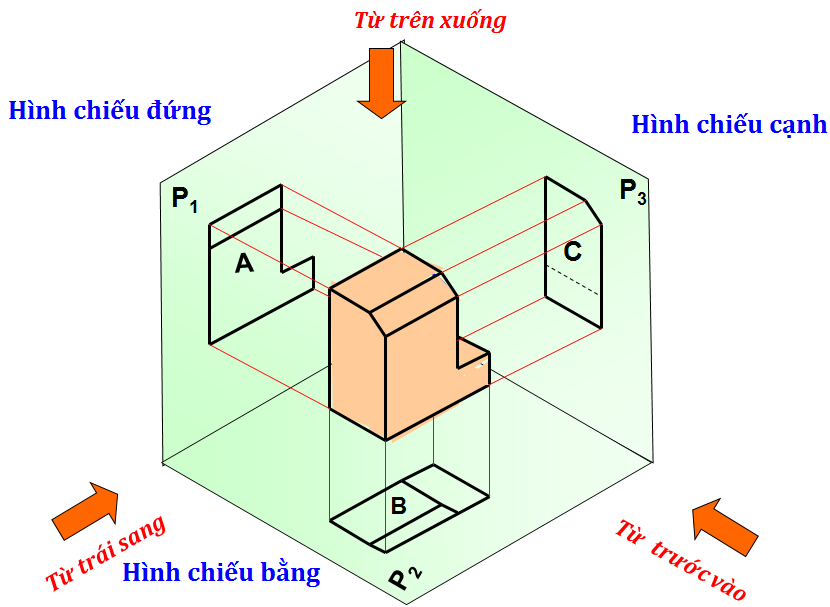
1/ Các loại hình chiếu trục đo

1.1/ Khái niệm về hình chiếu trục đo

Các hình chiếu vuông góc thể hiện một cách chính xác hình dạng và kích thước của vật thể được biểu diễn, do đó trong kỹ thuật phương pháp hình chiếu vuông góc được lấy làm phương pháp biểu diễn chính.

Xong mỗi hình chiếu vuông thường chỉ thể hiện được hai chiều của vật thể, nên hình vẽ thiếu tính lập thể, làm cho người đọc khó hình dung hình dạng của vật thể.

>> Để khắc phục được nhược điểm đó của phương pháp hình chiếu vuông góc, người ta dùng phương pháp hình chiếu trục đo để biểu diễn bổ sung.

Hình chiếu trục đo thể hiện đồng thời trên một hình chiếu biểu diễn ba chiều của vật thể, nên hình vẽ có tính lập thể.

>> Vì vậy, trên các bản vẽ của các bản vẽ phức tạp, bên cạnh các hình chiếu vuông góc, người ta thường còn vẽ thêm hình chiếu trục đo của vật thể.

– Hình chiếu trục đo còn dùng để vẽ sơ đồ, phác thảo bộ phận trong giai đoạn thiết kế.

Nội dung của phương pháp hình chiếu trục đo được quy định trong TCVN 11-78

Căn cứ theo phương chiếu người ta chia ra:

Hình chiếu trục đo vuông góc: Phương pháp chiếu vuông góc với mặt phẳng hình chiếu.
Hình chiếu trục đo xiên góc: Phương chiếu không vuông góc với mặt phẳng hình chiếu.

Căn cứ theo hệ số biến dạng chia ra:

Hình chiếu trục đo đều: Ba hệ số biến dạng theo ba trục bằng nhau.
Hình chiếu trục đo cân: Hai trong ba hệ số biến dạng theo ba trục bằng nhau.
Hình chiếu trục đo lệch: Ba hệ số biến dạng trên ba trục tưng đôi một không bằng nhau

1.2/ Các loại hình chiếu trục đo

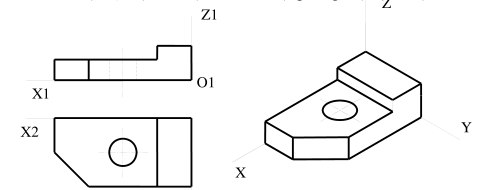
a/ Hình chiếu trục đo xiên góc Z

Định nghĩa d

Hình chiếu trục đo xiên góc là hình chiếu trục đo sử dụng phương pháp chiếu không vuông góc với mặt phẳng hình chiếu. Ta chia hình chiếu trục đo xiên góc này thành ba loại chính X sau: d

Hình chiếu trục đo đứng đều.
Hình chiếu trục đo đứng cân
Hình chiếu trục đo bằng đều.

Hình chiếu trục đo đứng đều

Hình chiếu trục đo đứng đều có vị trí các trục như hình 4.1

Các góc X’O’Y = Y’O’Z’ = 1350 và X’O’Z’ = 90o và các hệ số biến dạng quy ước p = q = r =1.

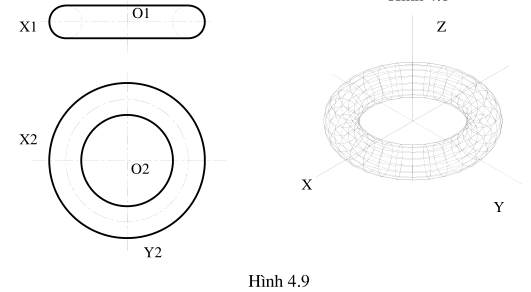
Trong hình chiếu trục đo đứng ( đều và cân) có mặt XOZ là mặt không bị biến dạng. Các đường tròn nằm trong mặt phẳng chiếu đứng có hình chiếu trục đo là các đường tròn. Các đường tròn nằm trong mặt phẳng song song với mặt phẳng hình chiếu bằng và hình chiếu cạnh thì có hình chiếu trục đo là dạng elíp.

Đối với hình chiếu trục đo đều, trục lớn của elíp = 1,3.d và trục nhỏ = 0,5.d ( với d là đường kính đường tròn). Trục lớn của elíp làm với trục O’X’ hay trục O’Z’ một góc 22o30’ tuỳ thuộc elíp thuộc mặt phẳng chiếu chứa trục O’X’ hay O’Z’.

Hình chiếu trục đo đứng đều thường dùng để thể hiện những chi tiết có chiều dài hay chiều dài nhỏ. Cho phép dùng hình chiếu trục đo đứng đều có trục O’Y’ làm với đường bằng một góc 30o hay 60o.

b/ Hình chiếu trục đo đứng cân.

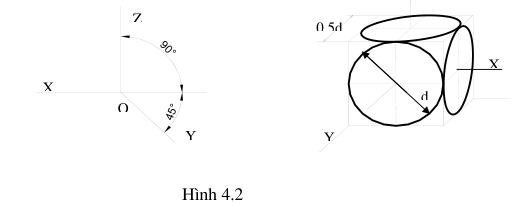
Loại hình chiếu đứng cân có vị trí các trục đo giống như các hình chiếu trục đo đứng đều. Các góc X’O’Y’ = Y’O’Z’ = 135o và X’O’Z’ = 90o. Các hệ số biến dạng quy ước p = r = 1 và q =0.5

Hình chiếu trục đo đứng cân của đường tròn nằm trong mặt đứng là mặt phẳng X’O’Z’ không bị biến dạng.

Các đường tròn nằm trong mặt phẳng song song với các mặt X’O’Y ‘ và Y’O’Z’ có hình chiếu trục đo đứng cân là elíp. Nếu lấy theo hệ số biến dạng qui ước ở trên thì ở trên thì trục lớn của elíp bằng 1,06.d và trục nhỏ bằng 0,35.d ( trong đó d là đường kính đường tròn). Trục lớn của elíp làm với trục O’Z’ một góc 70 .

Hình chiếu trục đo đứng cân thường thể hiện các chi tiết có chiều dài lớn.

Khi vẽ cho phép thay thế elíp bằng cách vẽ như hình 4.2 Z

c/ Hình chiếu trục đo bằng đều.

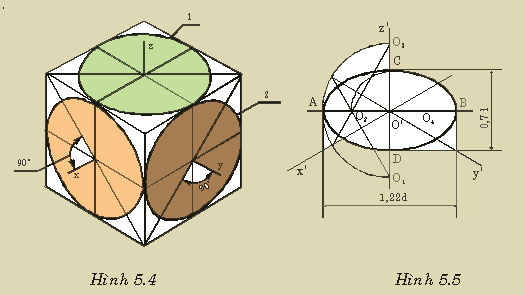
Loại hình chiếu trục đo bằng đều có vị trí các trục đo như hình vẽ số .. , các góc X’O’Y’ = 90, Y’O’Z’ = 120o và X’O’Z’ = 150o các hệ số biến dạng quy ước p = q = r = 0,94 và q = 0,47. xem hình 4.3

Trong hình chiếu trục đo bằng đều có mặt X’O’Y’ là mặt phẳng không bị biến dạng.

Các mặt tròn nămg trên các mặt phẳng song song nằm trong mặt phẳng toạ độ X’O’Y’ có hình chiếu trục đo là đường tròn. Các đường tròn nằm trong các mặt phẳng song song với các mặt phẳng toạ độ Y’O’Z’ và X’O’Z’ có hình chiếu trục đo là elíp.

Trục lớn của elíp trong mặt X’O’Z’ bằng 1,37.d và làm với trục O’Z’ một góc 150, trục nhỏ bằng 0,37.d. Trục lớn của elíp trong mặt Y’O’Z’ bằng 1,22.d và làm với trục O’Z’ một góc bằng 30o, trục nhỏ bằng 0,71.d ( d là đường kính đường tròn).

Các hình chiếu trục đo bằng đều còn gọi là hình chiếu trục đo quân sự, dùng để thể hiện các công trình quân sự, ít dùng trong bản vẽ kỹ thuật cơ khí.

d/ Hình chiếu trục đo vuông góc

Định nghĩa

Là hình chiếu trục đo được sử dụng phương chiếu vuông góc với mặt phẳng hình chiếu. Theo tính chất này người ta chia hình chiếu trục đo thành hai dạng chính sa:

Hình chiếu trục đo vuông góc đều
Hình chiếu trục đo vuông góc cân

Cách bố trí trục đo và hệ số hình biến dạng

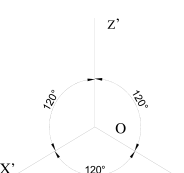
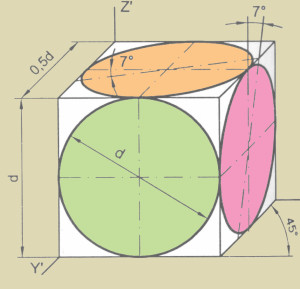
Hình chiếu trục đo vuông góc đều có vị trí các trục đo như hình 41, các góc X’O’Y’ = Y’O’Z’ = X’O’Z’ = 120 0 và các hệ số biến dạng theo các trục O’X’, O’Y’, O’Z’ là p = q = r = 0,82. xem hình 4.4 và 4.5

Để tiện vẽ người ta sử dụng hệ số biến dạng theo qui ước p = q =r = 1. Với hệ sô biến dạng quy ước này hình chiếu trục đo được xem như phóng to lên 1:0.82 = 1.22 lần so với thực tế.

Trong hình chiếu trục đo vuông góc đều, đường tròn nằm trong mặt phẳng song song với các mặt xác định bởi hai trục toạ độ có hình chiếu trụ đo là elip , trục lớn của elíp này vuông góc với hình chiếu trục đo của toạ độ thứ ba.

Nếu ta lấy các hệ số biến dạng p = q= r = 1 thì trục lớn của elíp bằng 1,22d và trục nhỏ của elíp bằng 0,7d ( d là đường kính đường tròn)

Trong các bản vẽ kỹ thuật, cho phép thay hình elíp bằng hình ô van cách vẽ như sau:

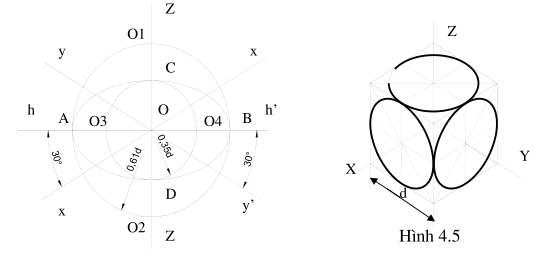
Bước 1: Dựng hai đường vuông góc zz’ và hh’
Bước 2: Dựng hai tia xx’ và yy’ tạo với hh’ một Z’ góc bằng 30o và -30o như hình vẽ.
Bước 3: Dựng đường tròn tâm O đường kính 1,22d cắt trục zz’ tại O1 và O2, cắt hh’ tại A và B và đường tròn tâm O đường kính 0,7d cắt trục zz’ tại C và D, cắt hh’ tại O3 và O4.
Bước 4: Lấy O1 làm tâm vẽ cung tròn bán kính O1C và lấy O2 làm tâm vẽ cung tròn bán kính O2D
Bước 5: Lấy O3 làm tâm vẽ cung tròn bán kính O3A, lấy O4 làm tâm vẽ cung tròn bán kính O4B.

>> Ta xác định được hình elíp cần vẽ.

d/ Hình chiếu trục đo vuông góc cân

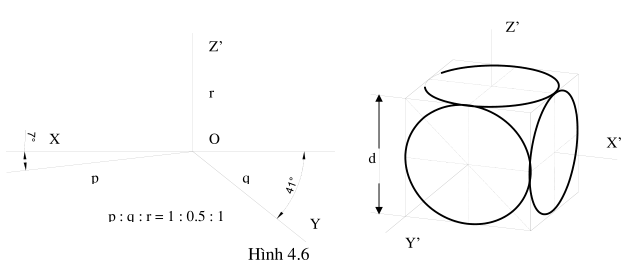
Hình chiếu trục đo vuông góc cân có vị trí trục đo như hình .. . các góc X’O’Y’ = Y’O’Z’ = 131025’ và X’O’Z’ = 97010’. Xem hình 4.6

Các hệ số biến dạng p = r = 0,94 và q = 0,47. Để tiện vẽ ta thường sử dụng hệ số biến dạng quy ước p = r = 1 và q = 0,5. Trục X’O’ được vẽ theo tg70 = 1:8 và trục O’Y’ vẽ theo tg41o = 7:8.

Với hệ số biến dạng qui ước thì hình chiếu trục đo coi như được phóng to lên 1: 0.94 = 1,06 lần, do đó trụ lớn của elíp bằng 1,06d và trục nhỏ bằng 0,94d hay 0,35d tuỳ theo elíp thuộc mặt phẳng nào.

e/ Các quy ước về hình chiếu trục đo

Theo TCVN 11-78 quy định về các quy ước vẽ hình chiếu trục đo như sau:

Trong hình chiếu trục đo các thành mỏng, các nan hoa .. vẫn vẽ ký hiệu vật liệu trên mặt cắt khi cắt dọc hay cắt ngang.
Trong hình chiếu trục đo cho phép cắt riêng phần, phần mặt cắt bị mặt phẳng trung gian cắt qua được quy ước bằng các chấm nhỏ.
Cho phép vẽ ren và răng của bánh răng.. theo quy ước như trong hình chiếu vuông vuông góc. Khi cần có thể vẽ hình chiếu trục đo của bước ren hay vài răng.
Đường gạch gạch trong hình chiếu trục đo được kẻ song song với hình chiếu trục đo của đường chéo của hình vuông có các cạnh song song với trục toạ độ tương ứng.
Khi ghi kích thước trên hình chiếu trục đo, các yếu tố kích thước như đường dóng, đường kích thước, mũi tên, chữ số kích thước được kẻ và viết theo nguyên tắc biến dạng của hình chiếu trục đo.

2/ Cách dụng hình chiếu trục đo

2.1/ Chọn loại hình chiếu trục đo

Để biểu diễn vật thể ta có thể dụng các loại hình chiếu trục đo trên, tuy nhiên tuỳ theo cấu tạo và hình dạng của từng vật thể và tuỳ theo các mục đích khác nhau mà ta chọn loại hình chiếu trục đo cho phù hợp, tức là ta dùng hình chiếu trục đo sao cho nó thể hiện được gần đúng nhất, dễ đọc nhất và đồng thời dễ thể hiện vật thể nhất.

Muốn thể hiện được vật thể có nhiều đường cong phức tạp, có hình dạng phức tạp ta nên dùng hình chiếu trục đo xiên và đặt các mặt đó song song với mặt không biến dạng, tuỳ theo chiều dài vật thể mầu ta đặt hình chiếu trục đo là xiên cân hay xiên đều.

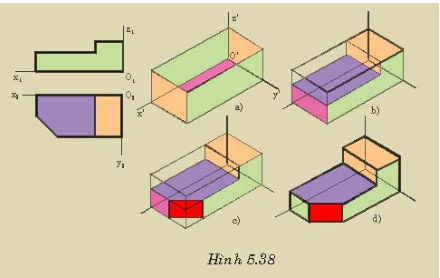
2.2/ Dựng hình chiếu trục đo a. Phương pháp toạ độ

Đây là phương pháp cơ bản để dựng hình chiếu trục đo của vật thể. Vậy muốn thể hiện hình chiếu trục đo của một vật thể ta phải xây dựng trên cơ sở hình chiếu trục đo của điểm.

Giả sử ta dựng hình chiếu trục đo của điểm A, trước hết ta vẽ vị trí các trục đo và xác định toạ độ vuông góc của các điểm XA, YA, ZA sau đó căn cứ vào hệ số biến dạng của loại trục đo mà ta sử dụng bằng cách nhân toạ độ vừa xác định với hệ số biến dạng tương ứng. X’A = XA.p và YA’ = YA.q và ZA’ = ZA.r sau đó đặt chúng lên toạ độ trục đo. Ta được A’ là hình chiếu trục đo của A.