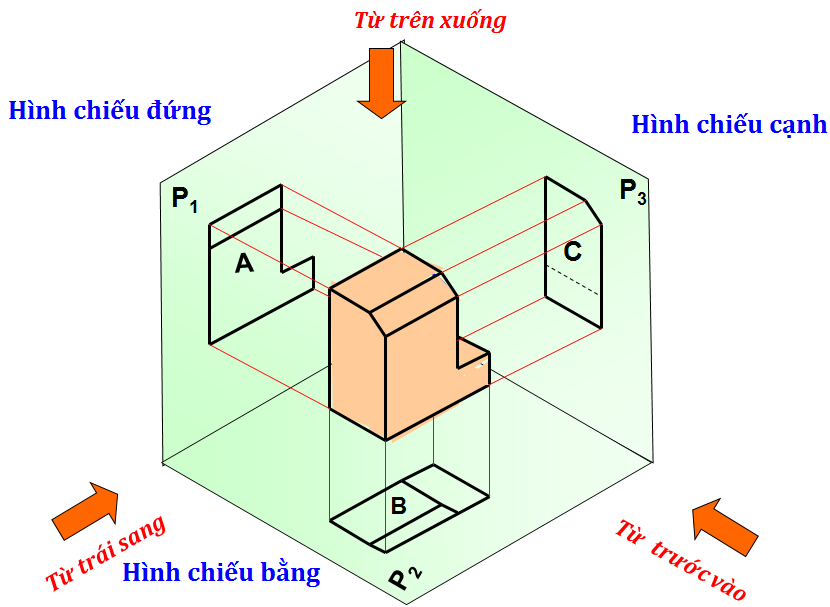
Tham số đặc trưng cho phân bố chuẩn của mẫu thử
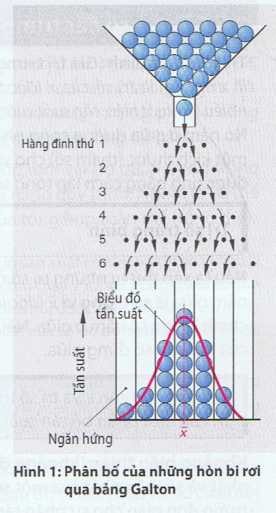
Trị số trung bình (Giá trị trung bình, tham số vị trí của phân bố) (đọc là x ngang) là trị số của x(đặc tính kiểm tra) khi đường cong mật độ (Độ nhiều, độ xuất hiện, tần suất xuất hiện) đạt đến điểm có độ xác suất cao nhất. Nó nằm ở giữa đường cong phân bố tần suất (hàm mật độ xác suất) và là một kích thước (tham số) cho vị trí của phân bổ (Hình 1).Trị số trung bình được tính bằng cách lập tổng số các trị số riêng lẻ x rồi chia cho cỡ mẫu n.
Nếu ta xếp thứ tự những trị số riêng lẻ của đặc tính từ nhỏ tới lớn thì trị số nằm giữa là số trung vị (đọc là x ngã). Nếu cỡ mẫu là số lẻ thì số trung vị chính là con số nằm ở giữa. Nếu cỡ mẫu là số chẵn thì ta lấy số trung bình của hai con số đứng giữa.
Trị số trung bình và trị số trung vị là hai đại lượng tiêu biểu cho vị trí của một phân bố tần suất xuất hiện và vì thế cho một quy trình.
Khoảng biến thiên (khoảng đo) R (phạm vi) là khoảng cách giữa số cao nhất và số thấp nhất của một sự lấy mẫu ngẫu nhiên. Nó là một trị số đặc trưng đơn giản cho sự phân tán của các trị số riêng lẻ.
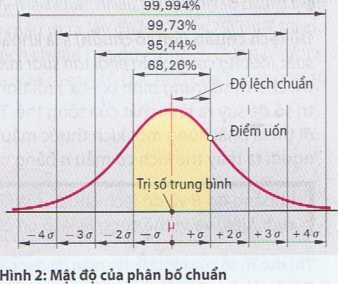
Độ lệch chuẩn (Sai số chuẩn) s là khoảng cách giữa trị số trung bình đến điểm uốn của hàm mật độ xác suất (đường cong phân phối tần suất xuất hiện) (Hình 1). Để tính độ lệch chuẩn ta lấy từng trị số riêng lẻ trừ cho trị số trung bình (xj– ) rồi tính ra bằng công thức của Hình 2.Ta có thể chỉ lấy một mẫu có vài trị số để suy ra tính chất của tổng thể. Tuy nhiên sự đánh giá này không chính xác. Muốn cho sai số nhỏ đi thì ta phải dùng một kích thước mẫu lớn hơn. Để cực tiểu hóa sai số khi dùng công thức trong Hình 2 người ta thay thế kích cỡ mẫu n bằng n-1.
Khoảng đo R và độ lệch chuẩn s là kích cỡ bể rộng của hàm mật độ xác suất (đường cong tần suất xuất hiện) và vì thế cũng là kích cỡ cho độ phân tán của các trị số riêng lẻ và của quy trình.
Thí dụ: Trị số của một lần lấy mẫu đã được xếp thứ tự: d, = 80,31; d2 = 80,42; dì = 80,44; d4 = 80,46; đ5 = 80,52;
Đánh giá: Trị số trung bình = (80,31 +80,42+80,44+80,46+80,52):5 = 80,43 mm;
Số trung vị = 80,44 mm;
Khoảng đo R= 80,52- 80,31 =0,21 mm;
Độ lệch chuẩn s = 0,077 mm
■ Trị số đặc trưng của phân bố chuẩn trong một lô kiểm tra
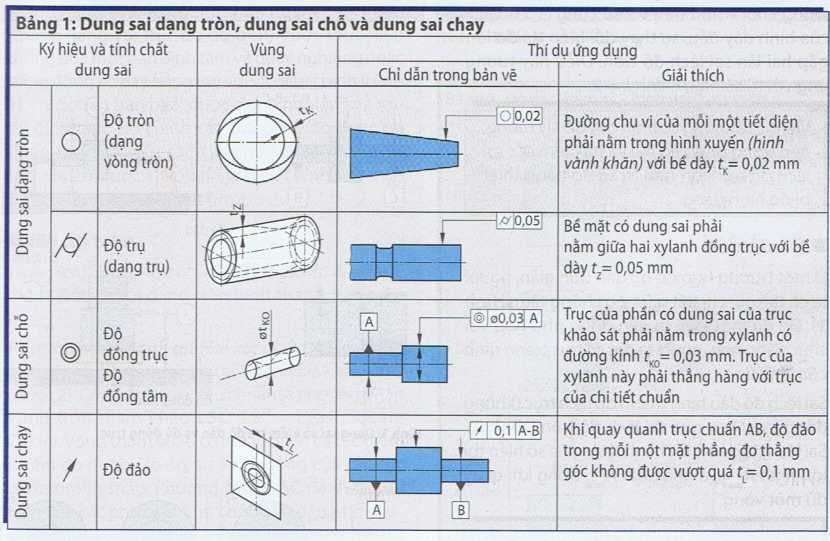
Ta có thể ước lượng trị số đặc trưng của toàn bộ tổng thể (lô kiểm tra) bằng phương pháp lấy mẫu và áp dụng những phép tính thống kê. Để phân biệt rõ ràng thông số ước lượng dựa trên tập hợp cơ bản (toàn bộ tổng thể) với thông số của mẫu lấy, người ta dùng những ký hiệu khác nhau. Để đánh dấu những trị số ước lượng người ta dùng dấu mũ A. Qua đó ta có thể phân biệt rõ ràng trị số ước lượng với trị số thực của quy trình. Trị số thực được tính bằng cách dùng phương pháp thống kê mô tả cho thử nghiệm 100% tổng thể (Bảng 1).